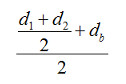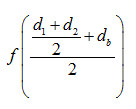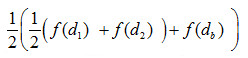Die Fassmessung
Die Notwendigkeit
Die kubische Visierrute
Die Visierschnur
Die quadratische Visierrute
Das Medial
Das teilgefüllte Fass
Visierer
Visierziffern und -zahlen
Visierbücher
Spätere Methoden
Literatur
Die Notwendigkeit
Im 14. und besonders im 15. Jahrhundert nimmt der Handelsverkehr erheblich zu. Betroffen ist auch der Transport von Wein. Handelszentren liegen in Süddeutschland - hier vor allem Regensburg, Nürnberg, Passau und Ulm - sowie in Österreich und entlang des Rheins bis Flandern. Nicht nur Käufer und Verkäufer müssen sich über die Menge des Handelsgutes einig sein, auch der Zoll und andere Abgaben entlang der Handelswege bemessen sich nach der Menge.
Wein wird fast ausschliesslich in Fässern transportiert. Sie besitzen
je nach Ursprungsort nicht nur verschiedene Grössen, sondern auch
unterschiedliche Formen bzw. Proportionen. Ein möglichst einfaches
Verfahren zur Bestimmung des Fassinhaltes wird gesucht. Daraus
entwickelt sich die Fassmesskunst, ein Teil der Visierkunst. Die
Visierkunst umfasst auch das Ausvisieren anderer Körper, etwa Zylinder
oder Kugeln. Verwendet wird ein langer Stab, genannt der
Visierstab oder die Visierrute, mit angepassten besonderen Skalen. Man
unterscheidet zwei Bauarten der Visierruten für Fässer, die auf
unterschiedlichen mathematischen Grundlagen aufbauen.
Die kubische Visierrute
Die kubische Visierrute basiert auf der Tatsache, dass sich die Volumina ähnlicher Körper verhalten wie die dritten Potenzen gleicher Strecken, allgemein V1/ V2 = (a1/a2)3. Von der dritten Potenz leitet sich die Bezeichnung kubische Rute ab. Für die Bestimmung des Fassinhalts genügt eine Messung. Üblicherweise misst man die Diagonale vom mittig gelegenen Spundloch zur gegenüber liegenden Ecke zwischen Boden und Seitenwand. Eine grosse Länge verringert die Gefahr von Fehlmessungen. Am unteren Rand des Spundlochs kann das Volumen des Fasses unmittelbar auf der Visierrute abgelesen werden. Wegen der dritten Potenzen der Längen sind die Werte auf der Skala ungleich verteilt und nehmen nach oben hin in immer kürzeren Abständen sehr schnell zu.
 |
| Der Gebrauch der kubischen Visierrute. Wie das
Bild richtig zeigt ist sie nach oben hin enger geteilt. (Ausschnitt des Titelblattes bei Schreiber 1523) |
Eine kubische Visierrute kann nur für eine Fassform berechnet und
ausgelegt sein. An einem Fass mit anderen Proportionen kann man sie
nicht verwenden.
Die kubische Visierrute wird nicht in allen Texten genannt. Nach dem
örtlichen Auftreten ihrer Beschreibungen zu urteilen ist sie erstmals
in Österreich aufgetaucht.
Das Teilen einer kubischen Rute ist nicht ganz einfach. Zunächst wird ein Normfass mit dem bekannten Volumen V in den ortsüblichen Einheiten diagonal ausgemessen und die Strecke auf einem Stab markiert. Als nächstes wird diese Strecke in 3√V Teile geteilt, deren Teilungspunkte, vom Anfang beginnend, mit 1, 8, 27, 64 usw.markiert sind. Für Zwischenwerte wird überwiegend eine Kubikwurzeltabelle verwendet.
Die Visierschnur
Es
handelt sich hierbei um eine längere Schnur, die mittels Knoten wie die
Kubikrute geteilt ist. Ihre erste Teilung wird an einem Fass mit
bekanntem Inhalt vorgenommen. Für die Visierung eines Fasses bestimmt
man das Mittel der Umfänge an beiden Böden sowie das Mittel dieser
Länge mit dem Umfang am Bauch des Fasses in der Mitte und addiert dazu
die Länge des Fasses. Der Endpunkt der addierten Strecken bestimmt das
Volumen des Fasses.
Der Vorteil dieser Methode besteht darin, dass das Fass zur Volumenbestimmung nicht geöffnet werden muss.
Beschreibungen des Verfahrens geben Helmreich 1557, Beutel 1735 und
Öchsner 1616. Letzterer führt die Teilung einer Schnur an einem
Beispiel mit realen Messwerten vor. Auch zeigt er die vollständig
geteilte Schnur in einer Abbildung (nur im Digitalisat der SLUB
vorhanden, unmittelbar nach der Einleitung).
 |
| Die Visierschnur bei Öchsner 1616, geeicht und geteilt auf Eimer und Kannen. Die untere Hälfte muss an der oberen rechts angefügt werden. Dann erhält man 6 Abschnitte der Schnur. |
Die Visierschnur basiert auf der Ähnlichkeit der Fässer, versucht
jedoch zwei Variable, nämlich mittlerer Durchmesser und Länge, zu
berücksichtigen. Sehr gross kann die Genauigkeit nicht gewesen sein.
Die Visierschnur wird nicht in allen Schriften genannt, Kern
beispielsweise beschreibt die Visierschnur in seinem umfassenden Werk
nicht.
Die quadratische Visierrute
Eine andere Konstruktion der Visierrute, die quadratische Rute, lässt sich universeller verwenden, weil sie nicht auf eine Fassform beschränkt ist. Ihre Anwendung setzt voraus, dass die Fassform auf einen Zylinder reduziert wird. Der Durchmesser des Zylinders entspricht dem Mittelwert aus dem grössten und dem kleinsten Durchmesser des Fasses. Die Länge des Zylinders ist identisch mit der inneren lichten Länge des Fasses. Mit Hilfe der folgenden Abbildung erläutert Kern in seinem Visierbuch die Reduktion auf einen Zylinder.
 |
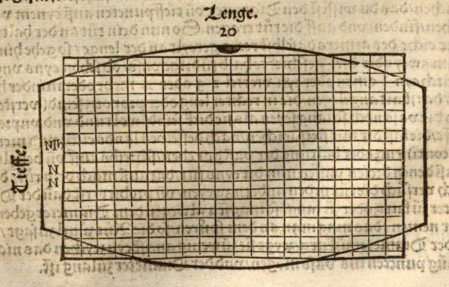| Die Reduktion des Fasses auf einen Zylinder bei Kern 1531 |
Die nächste Abbildung zeigt die Bestimmung der Fasslänge und eines
Fassdurchmessers. Für die Länge verwendet man Haken an beiden Böden,
weil die Dauben über die Böden überstehen. Vom Messwert muss die
doppelte Bodenstärke ebenfalls noch abgezogen werden.
 |
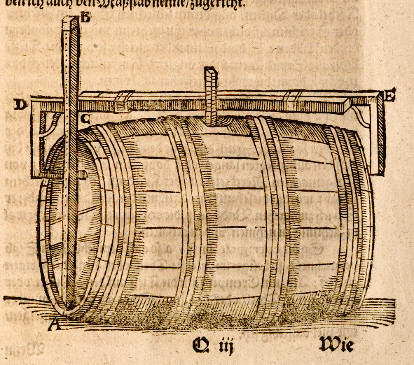| Messen der Fasslänge und des mittleren
Fassdurchmessers (identische Darstellung bei Zuccalmaglio 1607 und bei Galgemair 1655) |
 |
| "Liber maister fisirit mirs recht". Bestimmung
des Spunddurchmessers (aus dem Visierbüchlein von 1485) |
Der angenommene Durchmesser des Zylinders ist das arithmetische Mittel der beiden Fassdurchmesser in der Mitte und am Boden. Sind die Durchmesser der Böden ungleich wird zuvor von ihnen ebenfalls das arithmetische Mittel genommen. Die Durchmesser des Fasses werden auch Tiefe genannt. Zur Bestimmung des arithmetischen Mittels dient ein hierfür konstruiertes Instrument, das Medial (s. u.).
Zuccalmaglio 1607 gibt ein weiteres Verfahren zur Bestimmung des
mittleren Durchmessers an. Er misst ihn von aussen unmittelbar ohne
eine Mittelwertbildung. Wie in der Abbildung oben gezeigt stellt er
dazu die Tiefenrute auf die Dauben an einem Boden und misst die Höhe
bis zum Spundloch. Damit erhält er den mittleren Durchmesser aus dem
Bodendurchmesser plus der halben Differenz von grösstem Durchmesser
minus Bodendurchmesser. Er muss dann noch die Dicke der Dauben in der
Mite schätzen und abziehen. Sein Verfahren hat den Vorteil
dass das Fass nicht geöffnet werden muss.
Galgemair übernimmt Jahre später sowohl das Bild als auch den Text
wörtlich von Zuccalmaglio.
Man könnte den gesuchten Inhalt mit den gemessenen Werten für
mittleren Durchmesser und Länge und mit der Formel für das
Zylindervolumen berechnen. So wird jedoch nicht vorgegangen. Zum einen
sind Mehrfachrechnungen zu dieser Zeit am Ort der Messung nur mit
grossem Aufwand auszuführen. Des weiteren gibt es keine kohärenten
Masseinheiten, was zur Folge hat, dass beispielsweise zu Längen
gemessen in Ellen keine Masseinheit Kubikellen existiert. Das Volumen
wird in anderen Einheiten angegeben, was weitere Umrechnungen mit sich
brächte. Tatsächlich sind die Skalen der quadratischen Visierruten
anders aufgebaut.
Sie basieren auf dem Satz, dass das Volumen eines Zylinders
proportional ist zur Länge und zum Quadrat des Durchmessers. Die
Proportionalität D der Durchmesser und L der Längen beziehen sich auf
einen Zylinder mit bekanntem Inhalt und werden durch den zu messenden
Zylinder bzw. das Fass vorgegeben. Es gilt dann V~D2*L.
Als Basis für die Verhältnisse des Durchmessers und der Länge dient
entweder ein Normzylinder oder ein Fass mit bekanntem Inhalt. Auf der
Stabseite für die Messung der Tiefe werden die Proportionalitäten D
aufgetragen, allerdings benannt mit ihren Quadratzahlen 1, 4, 9, 16
usw. Dadurch erspart man sich nach dem Ablesen der Tiefe das
Quadrieren. Von dieser Quadratskala leitet sich der Name des
Instruments ab.
Einfache Stäbe tragen auf der Längenskala die Proportionalitäten für
die Länge. Die Teilung der Längenskala lässt sich leicht an die
Volumeneinheiten des Normzylinders anpassen. Man muss dann nur noch
beim Ausmessen eines Fasses die am Fass gemessene Zahl auf der
Quadratskala (die sog. Tiefenzahl) mit der auf der Längenskala
gemessenen Längenzahl multiplizieren und erhält das gesuchte Volumen.
 |
| Eine einfache
Quadratrute bei Kern 1531. An der Seite vorn die quadratische Tiefenskala, oben die Längenskala |
Der Rute im Bild oben liegt ein zylindrisches Gefäss mit dem
Durchmesser D und der Höhe L zu Grunde. Dieses fasst, hier als
Beispiel angenommen, vier Viertel eines Masses. Auf der Tiefen-
(Durchmesser)-Skala sind die Strecken vom Rutenanfang links bis 1*D,
2*D, 3*D... mit den Werten 1, 4, 9,... markiert. Auf der Längenskala
ist die Höhe des Normzylinders ebenfalls vom Rutenanfang weg als 1*L,
2*L, 3*L,... mehrfach aufgetragen, jedoch wegen der Einheit Viertel
mit den Zahlen 4, 8, 12,... markiert.
Multipliziert man die gemessene Tiefenzahl mit der gemessenen
Längenzahl, so erhält man sofort das gesuchte Volumen in Viertel.
In manchen Visierbüchern wird darauf hingewiesen, dass die Tiefenskala
auch linear geteilt sein kann. Dann muss man rechnen V = Tiefenzahl x
Tiefenzahl x Längenzahl.
Für die feineren Teilungen zwischen den Quadratzahlen auf der
Quadratskala werden geometrische Konstruktionen gelehrt oder Tabellen
mit Werten für Quadratwurzeln gegeben.
 |
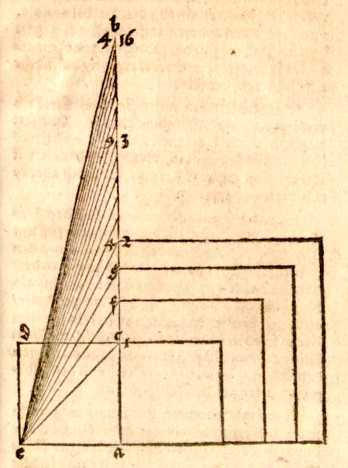| Die geometrische
Konstruktion einer Quadratskala √1, √2, √3, √4... bei Helm 1551 |
 |
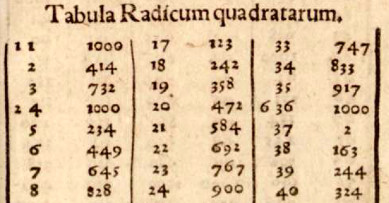| Eine Tafel mit
Quadratwurzeln (gekürzt) bei Helm |
 |
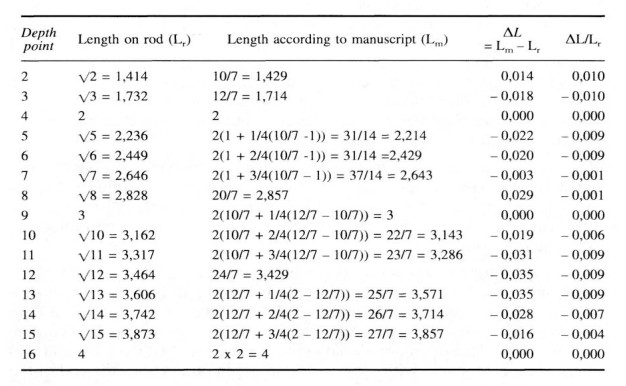| Ungewöhnliche
Näherungen für Quadratwurzeln, umgesetzt in
Teilungsvorschriften, im Damme Manuskript (aus Meskens 1999, S.
65f) In der Zeile des Tiefenpunktes 6 muss es heissen 34 / 7 |
Andere Quadratruten sind komfortabler ausgestattet. Die Längenskala trägt dort keine Zahlen für Vielfache. Stattdessen ist das Volumen direkt aufgetragen. Damit erspart man sich noch einmal eine Multiplikation. Allerdings gilt jede Volumenskala nur für eine bestimmte Tiefe. Deshalb tragen die Quadratruten mehrere Volumenskalen, sog. Wechsel. Die Quadratskala zeigt an, für welche Tiefen Wechsel eingerichtet sind. Wegen der Wechsel nennt man die quadratische Rute manchmal auch Wechselrute.
 |
| Die vier Seiten einer Quadratrute bei Kern
1531 Oben die Tiefenskala, darunter die Seiten mit den Wechseln |
In der Anwendung der Quadratrute können trotz aller Vereinfachung komplizierte Fälle auftreten, nämlich wenn es keinen Wechsel für die gemessene Tiefe gibt oder die Rute für die Fasslänge zu kurz ist. Auf solche Besonderheiten muss der Visierer vorbereitet sein, sie werden in den Visierbüchern behandelt.
Längen- und Tiefenskala müssen nicht auf dem gleichen Stab angebracht sein. Graffenried 1619 zeigt ein bemerkenswertes Bild (s. u.)
 |
| Visieren eines Fasses mit Längen- und Tiefenrute Aus Graffenried 1619, 4. Buch, S. 649 |
Der
Mann rechts hält die Längenrute mit ihrem Haken an den Fassboden. Der
Mann in der Mitte liest die Tiefe des Fasses durch das Spundloch ab.
Rechts hält einer eine Schreibunterlage und blickt dabei auf die
Längenskala. Offensichtlich notiert er die Messwerte und multipliziert
sie anschliessend.
Das Medial
Der Gebrauch der Quadratrute erfordert die Bestimmung des arithmetischen Mittelwertes zweier Durchmesser. Die beiden Strecken sind bei der Messung vom gleichen Anfangspunkt, dem Skalenanfang, aus aufgetragen. Im nächsten Schritt muss die Mitte zwischen beiden Endpunkten gefunden werden. Hierzu dient ein einfaches Hilfsmittel, ganz ähnlich einem Lineal, das von lat. medium (die Mitte) Medial genannt wird. Es trägt parallel angeordnet markierte Zahlenfolgen. Die Zahlen an jeder Stelle sind die Hälfte bzw. das Doppelte der benachbarten Zahl. Die Zahlenfolgen beginnen entweder in der Mitte des Lineals und verlaufen symmetrisch nach beiden Seiten wie bei Köbel oder Helm oder sie beginnen alle an der gleichen Schmalseite wie bei Beyer. Die Ausführungen der Mediale sind vielfältig.
 |
| Eines der Mediale bei Frey 1531 |
 |
| Das Medial bei Kern 1531 |
 |
| Das Medial bei Helm 1551 |
 |
| Ein seltenes, original erhaltenes Medial, erkennbar an den drei Sternen in der Mitte. Es ist ca. 28 cm lang und entspricht der Ausgestaltung wie bei Helm 1551, jedoch ohne Zahlen. |
 |
| Das Medial bei Helmreich 1557 |
Der Gebrauch des Medials ist einfach. Nach dem Markieren von Boden- und Spunddurchmesser an der Quadratskala besitzt man zwei Endpunkte, deren Mitte gefunden werden soll. Das symmetrische Medial verschiebt man solange, bis links und rechts seiner Mitte zwei gleiche Zahlen oder zwei gleiche Teilungen einer Skala auf die Endpunkte der Strecken zeigen. Dann markiert die Mitte des Medials auch die Mitte zwischen den beiden Streckenenden.
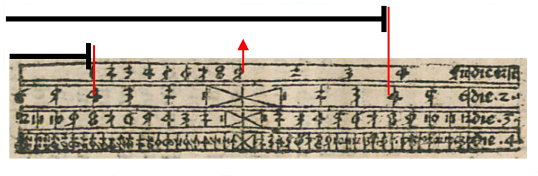
Oder man legt den Anfang der Skalen an ein Streckenende und liest am anderen Streckenende den dortigen Zahlenwert ab. Die gleiche Zahl auf einer anderen Skala mit doppelten Zahlenwerten aufgesucht markiert die arithmetische Mitte zwischen den beiden Streckenenden wie nachfolgend gezeigt.
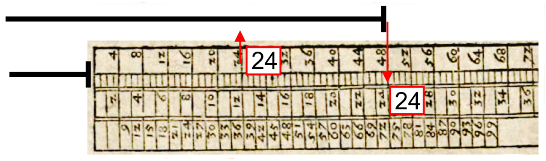
Wie auch die Visierruten ermöglicht das Medial die Lösung der Aufgabe
ohne jede Rechnung, die Kenntnis ihrer Handhabung und der Zahlen
genügt.
Ein weiterer Verwendungszweck des Medials bestand darin, dass man
damit Strecken aufnehmen und woanders hin übertragen konnte.
Im Zusammenhang mit dem Medial soll hier die Frage aufgegriffen
werden, welchen mittleren Durchmesser des Zylinders der Visierer
tatsächlich ermittelt.
|
Mit d1
und d2
als den Bodendurchmessern und db als dem
grössten (Bauch-) Durchmesser erhält der Visierer nach
zweimaliger Mittelwertbildung den neuen Durchmesser als Markierung auf der Quadratskala. Die zu diesem
Durchmesser gehörige Quadratzahl Der einzige mir bekannte Autor, der einen Mittelwert der auf der
Skala abgelesenen Zahlenwerte bildet , ist Graffenried 1619. Er erhält
somit Dieses Vorgehen ist jedoch eine grosse Ausnahme. |
Fässer waren damals schlanker als heute, d. h. Spund- und Bodendurchmesser näher beieinander.
Man kann daher für Quadratruten einen Messfehler von wenigen Prozent annehmen.
Das teilgefüllte Fass
Ein Problem blieb lange Zeit ungelöst: das liegende teilgefülltes
Fass. Hiefür wurden nur vereinzelt unterschiedliche Näherungsverfahren
gegeben.
Frey 1550 zitiert ein Verfahren des Rechenmeisters Erhard Helm aus
Frankfurt. Dieser bestimmt den Teilinhalt durch fortgesetze
Mittelwertbildung zwischen dem Boden- und dem Spunddurchmesser und der
Höhe des Flüssigkeitsstandes in der Mitte des Fasses. Das Ergebnis,
ein korrigierter Durchmesser, muss mit der Länge des Fasses
multipliziert werden. Seine Messung kann allenfalls eine Näherung
sein, weil sie, wie die Nachrechnung zeigt, den Extrema leeres und
volles Fass nicht genügt.
Beyer arbeitet in seiner Conometria Mauritiana 1619 mit einer Tafel von Kreissegmenten ("Schnitz-Täflin"). Er berechnet zunächst aus den Abmessungen des Fasses einen Zwischenwert. Mit diesem geht er in die Tafel und erhält den Prozentsatz der Füllung bezogen auf das ganze Fass. Seine drei Methoden erfordern viel Rechenarbeit.
Ähnlich wie Beyer geht Beutel 1672 vor. Er unterscheidet zwischen einer Teilfüllung mehr als die Hälfte und weniger als die Hälfte des Fasses. Durch mehrfache Mittelwertbildung und Subtraktion erhält er einen Zwischenwert, mit dem er, auf 1000 bezogen, in eine beigefügte Proportionaltafel geht. Die gibt ihm den prozentualen Teilinhalt des Fasses.
Erst als man in England ab Ende des 17. Jahrhunderts für die
Volumenbestimmung von Fässern Messstäbe und spezielle Rechenschieber (gauging rules) entwarf konnte auch diese
Aufgabenstellung bearbeitet werden (s. hierzu Lit. Thomas Everard,
1685, sowie Ron Manley's ausführliche Erläuterungen).
Visierer
Die Handhabung der Visierruten ist relativ einfach erlernbar. Man
muss nur ihre Anwendung kennen, die Ziffern beherrschen und
multiplizieren können. Kenntnisse ihrer Theorie erleichtern die
Arbeit, sind aber nicht erforderlich.
Visierer waren von der Stadt angestellt und mussten an Markttagen zur
Verfügung stehen. Naheliegend ist, dass diese Tätigkeit von den
Rechenmeistern ausgeführt wurde, die wegen ihrer besonderen Kenntnisse
auch für Ausbildung und andere Belange in Zusammenhang mit Arithmetik
zuständig waren. Helmreich 1557 beispielsweise nennt sich
"Rechenmeister und Visierer zu Halle in Sachsen". Wegen ihrer
verantwortungsvollen Tätigkeit, die von Kunden bezahlt werden musste
und die nur von ganz wenigen Kundigen der Materie durchschaubar war,
hatten sie einen Eid abzulegen. Er beinhaltete die Verpflichtung
richtig zu messen und richtig abzurechnen. Trotzdem sind nach Auskunft
von Prof. Menso Folkerts in Archiven zahlreiche Beschwerden über
Falschmessungen zu finden, die leider noch niemand ausgewertet hat. Das
verwundert nicht wenn man in der Widmung bei Beyer 1603 liest
"Wann
aber von denen Weinhändlern / sonderlich in jetzigen Jahren / da der
Wein hohes werths / täglich vielfaltige klage / der irrigen und
ungewissen Visierung halben / einkommen thut: auch in warheit nicht
ohne / daß bißweilln / theyls auß fahrläsigkeit und unvissenheyt
etlicher unachtsamen visierer / theyls auß ubel und fälschlich
zubereytete visierruthen / grosse mängel dißfals entstanden:..."
Falschmessungen werden wohl auch aus finanziellen Gründen vorgekommen
sein. Jedenfalls sind die oben geschilderten Gründe für Beyer Anlass, "die gantze Kunst des Visierens" darzustellen.
Meskens 1994 beschreibt die Situation der angestellten Visierer in Antwerpen um 1600 hinsichtlich ihrer Stellung und Aufgaben. Sogar ein Wettbewerb wurde veranstaltet. Absolut lesenswert. S. hierzu Details in Weiss, Stephan: Visieren und Streiten - Falschmessungen am Fass in der Frühen Neuzeit (12/2017) im Abschnitt Literatur.
Visierziffern und -zahlen
Der Mathematiker Rudolff (um 1500 - 1543?) berichtet, dass Visierer
besondere Ziffern verwendet haben, die nur für Kundige lesbar waren,
um das Volumen eines Fasses zu notieren. Das scheint auch ihr einziger
Verwendungszweck gewesen zu sein. Die Zahlen unterscheiden sich allein
in grafischen Elementen, ein Stellenwertsystem kann man damit nicht
aufbauen.
 |
Eine der Visierziffern bei Rudolff 1574. Das ganze |
Wir
haben hier einen jener seltenen Fälle vor uns, in dem ein Berufsstand
spezielle Zahlzeichen für seine Tätigkeit entwickelt hat, die von den
üblichen römischen oder indo-arabischen Ziffern grundlegend abweichen.
Es gibt kein einheitliches System der Visierziffern, sie unterscheiden sich von Region zu Region.
Visierbücher
 |
Wöltstu visieren manchen vaß/ |
Mit diesem Vers an den Leser beginnt Kern sein Visierbuch. Des Stabes Grund ist
nichts anderes als die theoretische Grundlage der Visierruten. Sein
Buch ist das umfassendste Werk über Visierruten, die er in zehn
Varianten einschliesslich ihrer Konstruktion beschreibt.
Genannt werden muss auch Beyer 1603. Seine Visierkunst beinhaltet
Stereometrie im allgemeinen, also nicht nur Fässer, sondern auch andere
Körper. Erwähnenswert ist, dass Beyer zu den wenigen gehört, der an
Stelle von geometrischen Konstruktionen rechnerischen Lösungen den
Vorzug gibt und sie vollständig nachvollziehbar darstellt.
Der früheste bekannte Hinweis auf einen eigenständigen Traktat über
das Visieren findet sich in einem Bücherkatalog der Abtei St. Emmeram
in Regensburg aus dem Jahr 1347. Ein weiterer sehr früher Hinweis auf
das Visieren mittels einer dazu gefertigten Rute (es ist eine
quadratische Rute) stammt aus der zweiten Hälfte des 14. Jahrhunderts.
Der Nürnberger Kaufmann Ulman Stromer (1329-1407) beschreibt sie in
seinen Aufzeichnungen Püchel vom meim Geslechet
und von abentewr (
Text).
Verständlich wird der Text allerdings nur wenn man weiss was gemeint
ist.
Meskens 1999 stellt eine ebenfalls frühe Beschreibung vor. Es handelt
sich um eine Handschrift aus dem Sint-Janshospitaal in Damme bei
Brügge. Sie datiert in das zweite Viertel des 14. Jahrhunderts. Das
Hospital besass zeitweise Visierrechte als Einnahmequelle. Die
Handschrift gehört zu einer der beiden, die bei King 2001 als Quellen
für Visierziffern aufgeführt sind.
Nach den oben genannten Texten zu urteilen muss die Visierrute bereits im 14. Jahrhundert in Gebrauch gewesen sein. Wann und wo sie erfunden wurde ist nicht bekannt.
Traktate über Visierruten sind entweder eigenständige Werke oder nur
kurz gefasste Abschnitte in Rechenlehrbüchern. Das Thema ist fester
Bestandteil der praktischen Arithmetik. Folkerts 1974 zählt 44
Handschriften und 22 gedruckte Darstellungen - sofern es sich um
selbständige Werke oder längere Abschnitte in anderen Werken handelt -
zur Visierkunst bis in das Jahr 1666 auf.
Inhaltlich beschränken sich die Autoren auf rezeptartige
Beschreibungen der Konstruktion und der Anwendung von Ruten. Manche
Autoren erläutern einen Rechengang zunächst allgemein und führen ihn
dann nochmals mit vorgegebenen Zahlenwerten aus. Darüber hinaus
gehende Erläuterungen oder Begründungen werden nicht gegeben. Für die
Anfertigung ungleicher Teilungen und die Interpolationen in Skalen
werden geometrische Konstruktionen vorgeführt oder vorgefertigte
Tabellen gegeben.
Der berühmte Astronom Kepler befasste sich ebenfalls mit der
Bestimmung des Volumens von Fässern. Mit seinem Werk Nova
stereometria doliorum vinariorum stellt er die
Volumenbestimmung erstmals auf eine wissenschaftliche Ebene. Welche
Veranlassung er hatte, sich mit diesem Thema zu beschäftigen, erklärt
er gleich in der Einleitung. Bei Klug 1908 ist dieser Abschnitt
vom Lateinischen in das Deutsche übersetzt. Was Keplers Braut dazu
sagte als er sich schon während der Hochzeit Gedanken über das
Ausmessen von Fässern machte ist nicht überliefert.
Nach Keplers Beschreibung hat der Visierer eine kubische Rute verwendet. Das zweimalige diagonale Messen nach beiden Seiten dient der Prüfung des Fasses auf Symmetrie und vermindert den Messfehler.
Spätere Methoden
Ab dem 18. Jahrhundert werden die geometrischen Konstruktionen der
Skalen mit Hilfe eines Vergleichsgefässes ersetzt durch die
rechnerische Bestimmung der Skalenteilungen. Man berechnet den
Durchmesser oder die Länge eines Zylinders mit vorgegebenem Volumen,
der Masseinheit, bei frei gewähler Grösse der anderen Dimension.
Beispiele für dieses Vorgehen gibt u. a. Nicolas Bion.
In England, dem Ursprungsland des logarithmischen Rechenschiebes,
beginnt ab Ende des 17. Jahrhunderts mit den Vorschlägen von Thomas
Everard eine neue Methode des Visierens von Fässern. Die Form des
Fasses wird in vier Typen eingeteilt, Rechnungen werden von da an mit
Hilfe eines angepassten Rechenschiebers (gauging
rule) ausgeführt. Ron Manley's Webseite und die Vorträge von Werner Rudowski (s. Literatur) geben hierzu gute
Erläuterungen.
Literatur
=== weiterführende Literatur:
Folkerts, Menso: Die Entwicklung und Bedeutung der Visierkunst als
Beispiel der praktischen Mathematik der frühen Neuzeit. In: Humanismus
und Technik, Bd. 18 (1974), S. 1-41
Das
Standardwerk mit zahlreichen Quellenangaben
Folkerts, Menso: Die Fassmessung (Visierkunst) im späten Mittelalter und in der frühen Neuzeit. In: Gebhardt, Rainer (Hrsg.): Visier- und Rechenbücher der frühen Neuzeit (Schriften des Adam-Ries-Bundes Annaberg-Buchholz Bd. 19) 2008
King, David A.: The Ciphers of the Monks – A forgotten number
notation of the Middle Ages. 2001
s.a.
King
Leibowitz, Grete: Die Visierkunst im Mittelalter. Diss. Heidelberg
1933
Univ Heidelberg
Ron Manley's Slide Rule Site Gauging Rules
Martin, Tom: Gauging: The Art behind the Slide Rule
Artikel aus Brewery History 133 (2009), pp. 69-86
Meskens, Ad et al: Wine-Gauging at Damme [The evidence of a late
medieval manuscript]. In: Histoire & Mesure, 1999, volume 14 -
n°1-2. Varia. pp. 51-77.
Artikel
Meskens, Ad: Wine Gauging in Late 16th- and Early 17th-Century Antwerp. In: Historia Mathematica 21 (1994), pp. 121-147
Artikel
Peters, Gunthild: Zwei Gulden vom Fuder. Mathematik der Fassmessung und praktisches Visierwissen im 15. Jahrhundert. 2018
umfassendes Standardwerk
Röttel, Karl: "Arithemtica applicirt": Visierkunst, Buchhaltung, Kartographie und Astronomie bei Henricus Grammateus. In: Heinrich Schreyber aus Erfurt, genannt Grammateus. Algorismus - Studien zur Geschichte der Mathematik und der Naturwissenschaften, Heft 20, 1996
Rudowski, Werner:
Von Kilderkins, Hogsheads, Proof & Excise Officers (2007)
Foliensatz
Rudowski, Werner: Robert Burns (1759-1796) Der Poet und sein Rechenschieber (2013)
Foliensatz
Rudowski, Werner: Cast Gauging in Germany - without and with Slide Rules (2019)
Artikel
Schuppener, Georg: Visierbücher als frühneuhochdeutsche Fachtextsorte. In: Leipziger Arbeiten zur Sprach- und Kommunikationsgeschichte 15: Fachtextsorten - gestern und heute, 2008
Sterner, Matthäus: Geschichte der Rechenkunst, 1891
Univ Bielefeld
Storeck, Gunthild: Zahlentafeln in der Fassmessung des 15. Jahrhunderts. In: Arithmetik, Geometrie und Algebra der frühen Neuzeit, Bd. 23 der Schriften des Adam-Ries-Bundes e.V. Annaberg-Buchholz, 2014
Weiss, Stephan: Die Rekonstruktion eines Visierstabes (9/2022)
www.mechrech.info
Weiss, Stephan: Additive und subtraktive Maßangaben am
Beispiel
der Visierziffern (6/2018)
www.mechrech.info
Weiss, Stephan: Visieren und Streiten - Falschmessungen
am Fass
in der Frühen Neuzeit (12/2017)
www.mechrech.info
Weiss, Stephan: Ausführungen und Gebrauch des Medials (6/2017)
www.mechrech.info
Weiss, Stephan: Visierinstrumente zur Volumenbestimmung -
ein Überblick (12/2015)
www.mechrech.info
=== eine Auswahl historischer Visierbücher:
Anonym: Visierbüchlein. [Bamberg] 1485
MDZ
Beutel, Tobias: Geometrischer Lust-Garten. Dresden 1672
MDZ
Beutel, Tobias: Neu aufgelegte Arithmetica. Leipzig 1735
Google
Beyer, Johann Hartmann: Ein newe und schöne Art der vollkommenen
Visier-Kunst... Frankfurt/M. 1603.
(auch beigebunden bei Öchsner, s.u.)
SLUB
Beyer, Johann Hartmann: Conometria Mauritiana. Frankfurt/M. 1619.
MDZ
Bion, Nicolas: Neu-eröffnete mathematische Werck-Schule [Uebers.:
Johann Gabriel Doppelmayr], 2. Aufl., Nürnberg 1717
ETH
Everard, Thomas: Stereometry, or the art of gauging made easy, by the
help of a sliding-rule, which shews the area's of circles in gallons,
and the square and cube-root of any number under 100000, by inspection
...
London 1685 u.ö.
1705 Google , London 1750 Google MDZ
Frey, Johannes ; Pencz, Georg: Ein new Visier büchlein : welches
jnnhelt wie man durch den Quadraten auff eines jeden Lands Eych ein
Rutten zu beraytten und damit yetlichs unbekants Faß Visieren, Vnd
solches jnnhalt erkennen soll.Nürnberg 1531, 1550
MDZ
Galgemair, Georg: Kurtzer gründlicher gebesserter unnd vermehrter
Underricht ... proportional Schregmäsz und Circkels, Ulm, 1615
ETH
u. ö.,
Galgemair, Georg: Organon logikon : Herrn Georgij Galgemayrs kurtzer
gründlicher, warhaffter, gebesserter und vermehrter Underricht, Zu
Beraitung und Gebrauch deß Circkels, Schregmeß und Linial, in wahrer
Proportion schöne mathematische Kunststuck ..., 1626 u.ö.,
1655
ECHO SLUB
Graffenried,
Johan Rudolff von < Adeliger, Schultheiss von Bern, Schweiz >:
Arithmeticae logisticae popularis libri IIII, in welchen der
algorithmus in gantzen zahlen und fracturen ... gantz verständlich ...
erklärt. Bern 1619
ETH
Helm, Erhart: Visierbuch. Beigebunden zu einigen Ausgaben von Ries,
Adam: Rechenbuch auff Linien und Ziphren... Frankfurt/M. 1551 u.ö.
(auch als Faksimile erhältlich)
MDZ
Helmreich, Andreas: Ein new Visier-Büchlein. Eisleben 1557
MDZ
Kepler, Johannes: Nova stereometria doliorum vinariorum. Linz 1615.
Dt. Klug, R.: Neue Stereometrie der Fässer. Leipzig 1908
archive
Dt. auch in Knobloch, Eberhard: Nova Stereometria Doliorum Vinariorum.
Zur Fassrechnung Johannes Keplers, 2000
Koebel, Jacob: Rechenbuch Auff Linien und Ziffern, Mit einem Visir
Büchlin Klar unnd verstendtlich fürgeben; Gerechnet büchlin auff alle
wahr und Kauffmanschafft ; Müntz Gewicht Elen unnd Maß viler Land und
Stett verglichen, Franckfort, 1549
MDZ
Kern, Ulrich / Enckhusen, Johann:
Eyn new künstlichs wolgegründts Visierbuch gar gewiß und behend, aus
rechter Art der Geometria Rechnung, und Cirkelmessen. Straßburg 1531
MDZ
Öchsner, Melchior: Visierkunst. Erfurt 1616
MDZ (beigebunden Beyer 1603), SLUB
Peter von Jülich: De modo mensurandi vasa. Ein Traktat zur Fassmessung aus dem frühen 15. Jahrhundert. Herausgegeben, übersetzt und kommentiert von Menso Folkerts und Martin Hellmann. Algorismus, Heft 85 (2018)
Rudolff, Christoff: Kunstliche Rechnung mit der Ziffer vnd mit den
zal Pfennigen. Augsburg 1574 u.ö.
MDZ
Schreiber, Heinrich (Grammateus): Ein new künstlich ...
Rechenbüchlin. Erffurdt 1523
MDZ
Ulman Stromer's Püchel vom meim Geslechet und von abentewr (1360).
In: Die Chroniken der Fränkischen Städte, 1. Bd., Leipzig 1862
Google
Vaerman, Jan: Academia mathematica of Oeffen-school van de wis-konst,
1720
Google
Vulpius, Johann: Neu ausgefertigter In Eimern, Kannen und ihren Nösseln gantz richtiger Wein-Visierer..., 1691
SLUB
Zuccalmaglio, Anton Wilhelm Florentin von; Weiler, Jakobine: Kurtzer
Bericht, wie man die verschloßne Weinfässer ohne eröffnung deß Spondts
soll Visieren. Augsburg 1607
MDZ
xxx