. |
|
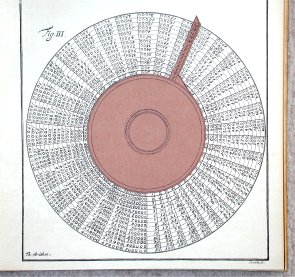
| Jacob Leupold zeigt diese Rechenscheibe in seinem
'Theatrum Arithmetico-Geometricum' von 1727, Tab. III, S. 17. Als Quelle gibt er Georg
Philipp Harsdoerffers 'Mathematische und philosophische Erquickstunden' von 1636 an. Erfinder der Scheibe soll ein französischer Rechenmeister gewesen sein.*) Positioniert man den drehbaren Zeiger neben eine der radialen Spalten, dann stehen neben den Produktfaktoren auf dem Zeiger die Vielfachen des anderen Produktfaktors im innersten Ring dieser Spalte. Die Stufung der Produktfaktoren auf dem Zeiger 241 x 36 = Auf diesem Weg wird das Multiplizieren auf ein Addieren
zurückgeführt. Auffallend ist, dass der Erfinder die konsequente Anwendung des
Stellenwertsystem vermeidet (sonst hätte eine Einmaleinstafel auch genügt).
Offensichtlich wollte der Erfinder mit dieser Rechenscheibe sowohl das Kleine Einmaleins
als auch die stellenrichtige Addition von Teilprodukten beim Multiplizieren durch ein
Rechenhilfsmittel ersetzen. Diese Absicht geht auch aus der Überschrift zum originalen Kapitel bei Harsdörffer hervor und lässt Rückschlüsse auf die Einschätzung
des Kenntnisstandes der möglichen Benutzer zu. Das Bild auf S. 49 zeigt eine Rechenscheibe identisch mit der bei Leupold, auf der in 37 Radialen untereinander die 1 - 9, 10, 20, 30, 40, 50-fachen der Zahlen Nach dem Text bei Harsdörffer zu urteilen hat es noch eine Scheibe mit den Vielfachen von 10000 bis 100 Millionen gegeben. |