1614 - 2014: 400 Jahre Logarithmen - John Napier und sein Werk
Eine Erinnerungsveranstaltung am 30.6.2014 in Gröbenzell
Textbuch

|
1450 entstand in Mainz der Buchdruck mit beweglichen Metalllettern durch Johannes Gensfleisch, genannt Gutenberg (geboren um 1400 – gestorben 1468)
1492 erfolgte die Entdeckung Amerikas durch Christoph Kolumbus (um 1451 – 1506), als Beginn der Erschließung der Kontinente zur See über Sterne-Navigation – Dadurch wurde der weltweite Handel intensiviert.
1517 war Anschlag der 95 Thesen in Wittenberg durch Martin Luther (Augustinermönch in Erfurt, geboren 1483 – gestorben 1546) läutete die Reformation ein.
1518 veröffentlichte Adam Ries (1492/3 – 1559) die erste Ausgabe „Das Rechnen auf den Linien“ in deutscher Sprache und lehrte als Rechenmeister in Erfurt.

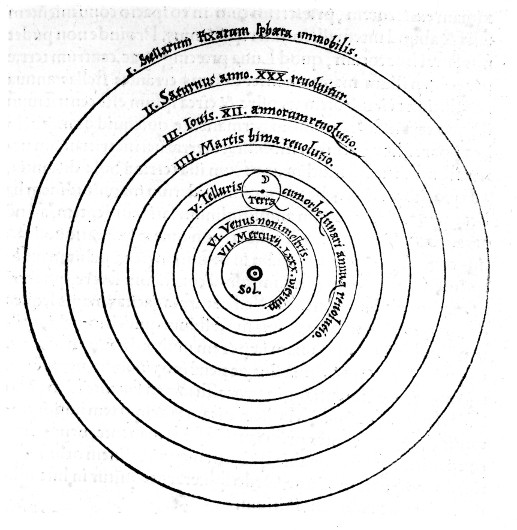
1543 brachte Nikolaus Kopernikus (1473 – 1543) „De revolutionibus orbium coelestium“ heraus, in dem er beschrieb, dass sich die Erde um die Sonne dreht. Für diese Veröffentlichung spielte Georg Joachim Rheticus aus Feldkirch (1514 – 1574) eine wichtige Rolle.
1544 kam von Michael Stifel (1487 – 1567; zunächst Augustinermönch in Esslingen) die „Arithmetica Integra“ heraus, in der er das Prinzip der Logarithmen herausgearbeitet hat.

Was war zu dieser Zeit in England bzw. Schottland los ?
Wechselnde Machtverhältnisse zwischen Katholiken (von Spanien unterstützt), Protestanten und Anglikanern. Es fanden heftige Kämpfe zwischen England und Spanien statt, die
1588 zur Vernichtung der spanischen Armada durch die englische Flotte führte.
In dieser Zeit wurde John Napier, Lord of Merchiston geboren. Wir haben das Glück, ihn über sein Leben ihn selbst zu befragen.
Willkommen, Sir John !
(Napier tritt auf)
Ladies and Gentlemen, glad to be here and many thanks for the invitation.
Über mein Leben gibt es nichts Wesentliches zu sagen.
Geboren wurde ich im Jahr 1550 in Merchiston Tower in Edinburgh, Schottland.
(† 3. April 1617)
Mein Vater war Sir Archibald Napier of Merchiston, meine Mutter Janet Bothwell. Beide waren bei meiner Geburt noch sehr jung. Ich hatte Bruder und Schwester.
Ich habe spät, mit 13, zu studieren begonnen an der St. Andrews Universität und lebte im St. Salvator's College. Dort wurde mein Interesse an Theologie geweckt. Der übrige Lehrstoff konnte jedoch meinen Wissensdrang nicht befriedigen. Deshalb habe ich diese Schule verlassen, war dann unerkannt in Europa unterwegs und habe dabei an Universi-täten meine Studien vertieft.
Mit Bescheidenheit gesagt besitze ich Kenntnisse in Theologie und Mathematik und ich beherrsche Griechisch und Latein.
Im Alter von 21 bin ich nach Schottland zurückgekehrt, habe geheiratet und lebte zunächst ein paar Jahre an einem anderen Ort. Nach dem Tod meines Vaters 1608, Gott habe ihn selig, habe ich Merchiston Castle sowie ein beträchtliches Vermögen geerbt.
Übrigens - Merchiston Tower of the Castle steht heute noch und ist der Kern der 1964 gegründeten Napier University in Edinburgh.
Ich habe dieses Schloss dann niemals mehr verlassen, Reisen liegt mir nicht so. Ich lebte dort als Laird oder landlord, als Gutsherr.
Verheiratet war ich zwei Mal.
(langsame Bewegung)
Ich bitte um Nachsicht, es ist die Gicht, die mir zu schaffen macht.
Theologie hat mich schon immer interessiert, vor allem in der Zeit religiöser Kontroversen und hierbei besonders die Offenbarung des Johannes.

Die Bibliothek der Napiers wurde Ende des 17. Jhd. bei einem Brand zerstört, so dass wir keine direkten Hinweise auf die von ihm verwendete Literatur haben.
Seit etwa einhundert Jahren bekämpfen sich in England und in Schottland Römisch-Katholische und Reformierte. Es geht die Angst um, dass die spanische Armada uns nochmals angreift und dass die Spanier England und Schottland erobern.
Ich habe zur Abwehr von Angriffen auch Waffen entworfen.
Zudem weiß niemand, wohin der wankelmütige König Jakob VI in Sachen Theologie tendiert.
Nun zur Offenbarung des Johannes.
Das ist der letzte Abschnitt in der Bibel. Ein durch und durch von Symbolen getragenes Werk göttlicher Offenbarung, etwa die vier apokalyptischen Reiter, das Buch mit den sieben Siegeln oder die Hure Babylon auf dem siebenköpfigen Tier.
Wenn uns Gott eine verschlüsselte Offenbarung gibt, dann müssen wir sie entschlüsseln, verständlich machen.
Ich bin überzeugter Reformierter, umso leichter war es mir, bei der Interpretation Abstand vom originalen Text zu wahren. Deshalb ist mir eine Interpretation gelungen. Auf Einzelheiten kann ich hier nicht eingehen.
Meine Niederschrift
A Plaine Discovery, of the whole Revelation of Saint John: set down in two treatises:
and so on has been published first in 1593. That is the first and only text I wrote in my first language for all people should be able to read the text ...
sorry, in German
Das Werk wurde 1593 publiziert.
Es ist das einzige Werk, das ich in meiner Muttersprache geschrieben habe, damit alle Menschen es lesen können. Ansonsten bevorzuge ich Latein, weil diese Sprache für die Wissenschaft präziser ist und von allen Wissenschaftlern gelesen werden kann.
Was ist uns offenbart worden? Hier nur zwei wesentliche Punkte:
Das jüngste Gericht wird um 1688 oder 1700 auf uns hernieder kommen.
Christus ist König der Könige und Herr der Herrscher
(redet sich in Rage).
Das siebenköpfige Tier, das ist Rom, die röm. katholische Kirche, von dort kommt das Übel...
Ich möchte das hier beenden. Wir wollen diesen Sachverhalt jetzt nicht weiter vertiefen. Das ist ihre Interpretation. Aber, Sir John, Sie haben doch auf dem Gebiet der Mathematik Wertvolles geleistet. Lassen Sie uns doch darüber sprechen.
Für Astronomen gestalten sich Multiplikationen und Divisionen mehrstelliger Zahlen schwierig, weil sphärische Trigonometrie zu Grunde liegt.Sie verwenden derzeit die sogenannte prosthaphäretische Methode
Das Wort leitet sich ab vom Griechischen prosthesis (Addition) und aphaeresis (Subtraktion)
Sie stützt sich auf trigonometrische Beziehungen und vereinfacht Multiplikationen zu Additionen. Hier ein Beispiel, das sie sicher kennen:
sin a sin b = ½[cos(a - b) - cos(a + b)]
Die zwei Produktfaktoren werden auf Größen im Bereich zwischen 0 und 1 normiert, die zugehörigen Winkel a und b werden gesucht, addiert und subtrahiert. Dann sucht man wiederum deren Winkelfunktionswert auf, addiert oder subtrahiert, teilt durch 2 und erhält das gesuchte Ergebnis, das wieder zurück normiert werden muss.
Nicht gerade einfach.
Die Astronomen sind trotzdem froh, ein solches Hilfsmittel zur Verfügung zu haben und deswegen brauchen wir auch hochpräzise Winkelfunktionstafeln wie z.B. das Opus Palatinum von Georg Joachim Rheticus.
Ich dachte mir, das müsste noch einfacher gehen. Es sind nämlich schon lange die besonderen Eigenschaften in der Gegenüberstellung einer arithmetischen und einer geometrischen Zahlenfolge bekannt. Gemma Frisius, Simon Jacob und besonders Michael Stifel haben darüber geschrieben.
Ich zeigs mal:
(geht an die Tafel und schreibt)
b a d c
|
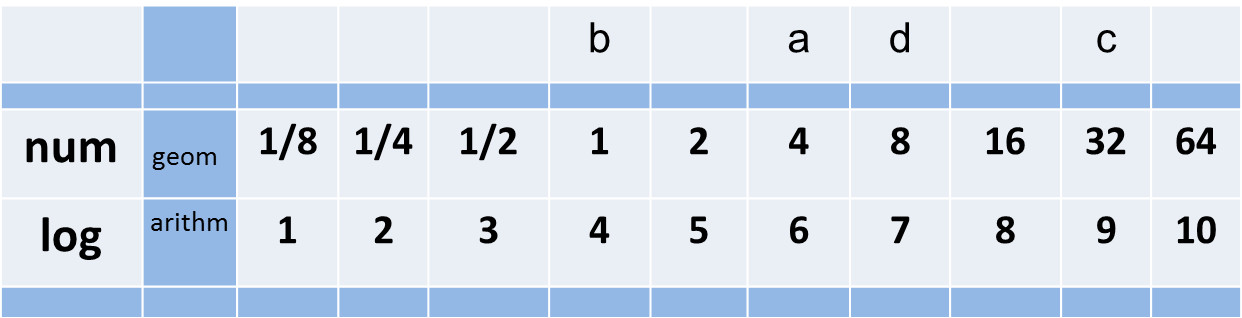
In der geometrischen Folge (oben) wird jeder Zahlenwert nach dem ersten durch Multiplizieren des vorherigen mit einem konstanten Zahlenwert gefunden. Das sind die Numeri.
In der arithmetischen Folge (unten) wird jeder Zahlenwert nach dem ersten durch Addieren des vorherigen zu einem konstanten Zahlenwert gefunden. Das sind die Logarithmen der Numeri.
Für 2 Zahlenpaare (a, b) und (c, d) gilt
wenn a/b = c/d dann auch log a – log b = log c – log d wegen der gleichen Abstände zwischen a und b sowie zwischen c und d
oder wenn a*d = b*c dann auch c = (a * d) / b .
(an der Tafel)
hier ein Rechenbeispiel für die Multiplikation. Wir müssen den Ansatz immer zurückführen auf die vollständige Definition, also
a*d = c*1
mit Zahlenwerten:
a = 4; d = 8; b = 1; c = ?
log c = log a + log d – log 1 = 6 + 7 – 4 = 9; log c = 9
und somit c = 32
Zu den sogenannten Logarithmen muss ich eines sagen:
das Wort stammt von mir, ich erfinde gerne neue Bezeichnungen und habe sie Proportionalzahlen genannt, abgeleitet von den griechischen Begriffen logos, das bedeutet Proportion, und arithmos, bedeutet Zahl.
Diese Logarithmuszahlen sind über Verhältnisse definiert. Sie stellen künstliche Zahlen dar, numeri artificiales, erfunden zur Vereinfachung von Multiplikationen oder Divisionen, eine andere Bedeutung besitzen sie nicht !
a/b = c/d → log a – log b = log c – log d
„Die Logarithmen haben das Leben der Astronomen verdoppelt, weil sie deren Arbeit halbiert haben“, sagte der berühmte Mathematiker und Astronom Pierre Simon Laplace (1749 – 1827) ca. 200 Jahre später.
Die Tafel oben im Beispiel ist zwar brauchbar, jedoch sind die Abstände zwischen den Eingängen zu groß, als dass man sie universell gebrauchen könnte.
(deutlich)
Die Tafel hat ein strukturelles Problem, kein prinzipielles.
Ich habe mir überlegt, wie man eine derartige Gegenüberstellung mit genügend feiner Stufung konstruieren könnte. Etwa 1594 hatte ich die Prinzipien meiner Logarithmen erarbeitet.
Für die Erstellung der Tafel bin ich von der Bewegung zweier Punkte ausgegangen. Einer bewegt sich mit konstanter Geschwindigkeit und stellt in bestimmten Zeitabständen die Numeri dar.
Der andere Punkt bewegt sich mit geometrisch proportional abnehmender Geschwindigkeit und stellt zu den gleichen Zeitpunkten die Logarithmen dar. D. h. ich bediene mich des Prinzips des Stetigen.
Man hätte ja die geometrische Folge auch durch fortgesetzte Multiplikation mit einer Zahl geringfügig über 1 berechnen können, aber das habe ich nicht getan. Für große Genauigkeit wäre die Rechenarbeit zu umfangreich geworden.
Dann musste ich sehr lange Zeit rechnen, es müssen so um die 20 Jahre gewesen sein. Schließlich war die Tafel fertig gestellt.
Eingänge in die Tafel sind die Winkel 0° bis 90° in Schritten von einer Minute und sie gibt die Werte für sinus und cosinus sowie deren Logarithmen.
Woher hatten Sie die Sinus-Werte?
Oder haben Sie diese gar selbst berechnet?
Die sinus-Werte sind aus den Tabellen von Fincke 1583 und denen von Lansberg 1591. Zuweilen habe ich verglichen, um Fehler auszuschließen.
Das Logarithmen-Werk ist 1614, also kürzlich erst, unter dem Titel Mirifici logarithmorum canonis descriptio herausgekommen. Beachten Sie bitte den doppelten vorangestellten Genitiv im Titel.
Hier sehen sie einen guten Vorabdruck, den ich mir behalten habe.
Mein verehrter Freund Edward Wright, der leider 1615 verstorben ist, hat eine sehr gute Übersetzung ins Englische verfasst.
Um Bruchzahlen zu vermeiden habe ich die Werte für einen Kreisradius von 10 Millionen angegeben.
(logNep 1 = 10^7 * 16,118089638 )
Log 1 ist ungleich 0.
(beschwichtigend)
ich weiß, ich weiß,
für Zahlen außerhalb des Wertebereichs der Winkelfunktionen wird die Anwendung der Logarithmen schwierig. Das ist zugegeben eine Schwäche meines Systems. Ich habe selbst schon an eine Änderung gedacht.
Aber: mit meinem System lassen sich trigonometrische Beziehungen leichter bearbeiten. Ich habe dazu einige trigonometrische Beziehungen den Logarithmen angepasst.
Und: weil log sinus totus, d.h. sin 90° gleich Null ist vereinfachen sich manche Berechnungen mit Logarithmen, in denen der sinus totus vorkommt.
Was Vor- oder Nachteile angeht, letztendlich gilt was ich schon in der descriptio geschrieben habe: Nihil in ortu perfectum das heißt nichts ist von Anfang an vollkommen.
Die Erläuterungen zu meinen Berechnungen mit dem Titel Mirifici logarithmorum canonis constructio sind auch schon fertig, sie werden demnächst erscheinen.
Ergänzen muss ich noch, dass bei einem Treffen mit meinem verehrten Freund und Kollegen Henry Briggs, Professor der Geometrie am damals wenige Jahre alten Gresham College in London, im Jahr 1615 wir uns über wesentliche Änderungen an einer zukünftigen Logarithmentafel einig wurden.
Und das kam so...

(Chronist zieht ein blau/grau kariertes Sakko an und wird Henry Briggs)
Nachdem ich John Napiers descriptio gelesen hatte, habe ich ihn besucht, weil ich von der Idee der Logarithmen begeistert war – mit einer Ausnahme. Deswegen habe ich zu ihm gesagt:
Sir John, sie setzen den Schwerpunkt der Anwendung der Logarithmen bei trigonometrischen Beziehungen. Rechnet man jedoch außerhalb des Wertebereichs des Sinus von 0 bis 1 wird es schwierig. Zudem werden über 1 bzw. über dem Radius 10 Millionen die Logarithmen negativ und sind damit schwerer zu handhaben.
log 1 = 10 bzw. 10 * Radius,
log 10 = 9 bzw. 9 * Radius und so fort bis log (10 Milliarden) = 0.
Das erleichtert das Rechnen in Stufen von 10.
log 1 = 0,
log 10 = 1 bzw. 1 * Radius,
log 100 = 2 bzw. 2 * Radius usw. setzen. Dann werden die Logarithmen für Zahlen größer 1 durchwegs positiv und der lästige Begleiter log 1 wird zu Null und tritt nicht mehr auf.
Ich bin zu alt, um die Arbeit an einer solchen Tafel nochmals auf mich zu nehmen.
(Chronist zieht sein Sakko wieder aus )
John Napier war gesundheitlich leider nicht mehr in der Lage, die Berechnungen wieder aufzunehmen. So hat Henry Briggs eine Neuberechnung der Tafel nach dem Vorschlag von Napier in einer Zuordnung begonnen, wie wir sie heute noch benutzen – The First Chiliad of Logarithmes 1617.

Zur Entwicklung und Wertung der Logarithmen sowie zu Napiers Ausführungen ist folgendes zu sagen:
Was Napier nicht wissen kann: zur gleichen Zeit berechnet Jost Bürgi (1552 – 1632), ein Schweizer, ebenfalls eine Logarithmentafel – die sog. Progresstabulen -, die anders aufgebaut ist als die von Napier. Er veröffentlicht sie jedoch erst später, nämlich im Jahr 1620 in Prag.

Die Veröffentlichung der constructio bzw. im vollen Titel Mirifici logarithmorum canonis constructio erlebt Napier nicht mehr, die veröffentlicht sein Sohn im Jahr 1619.
Die Definition der Logarithmen als Proportion in der Gegenüberstellung einer arithmetischen mit einer geometrischen Folge hält sich bis Anfang des 18. Jahrhunderts. Erst mit Übernahme des Konzepts einer Funktion und mit der Verwendung des Begriffs der Potenz etwa in der ersten Hälfte des 18. Jahrhunderts erhalten die Logarithmen die Definition, die für sie heute noch verwendet wird.
Die Logarithmen, die ehemals künstlichen Zahlen, sind längst keine solchen mehr, sie sind Bestandteil vieler Berechnungen und Formulierungen von Gesetzmäßigkeiten in Mathematik und Naturwissenschaften geworden.
Hier sei kurz die Geschichte der Tafeln einiger wichtiger Tafelmacher (Logarithmenberechner) erwähnt:
• Johannes Kepler (aus Deutschland) 1624
• Edzechiel de Decker und Adrian Vlacq (aus Holland) 1626
• Abraham Sharp (aus England) 1717
• Juri Vega (aus Slowenien damals bei Österreich; daher in Deutsch und Latein veröffentlichend) 1783
• Jean Peters (aus Deutschland) 1910
• Arnold Noah Lowan (aus USA – MTP) (LN) 1941
Ab dem 19. Jahrhundert erfolgt die Berechnung der Logarithmen mit mechanischer Hilfe, wie z.B. mit Differenzenmaschinen (Hamann und Thompson) oder mit Computern.

Sir John, sie hatten keine Möglichkeiten, sich das Rechnen zu vereinfachen.
Nein, ich hatte keine, deswegen habe ich mir Multiplizierstäbe als Berechnungshilfen gebaut...
Das Berechnen der Logarithmen war mühselig, das können sie sich nicht vorstellen. Alles mit der Hand zu rechnen brauchte jahrzehntelang; soweit ich mich erinnern kann, etwa 20 Jahre.
Ich habe daher eine einfache Rechenhilfe entworfen, die Rabdologia, auch so ein Kunstwort aus griechischen mit rabdos = Stab und logia = Das Wissen über..., Die Kenntnis von....
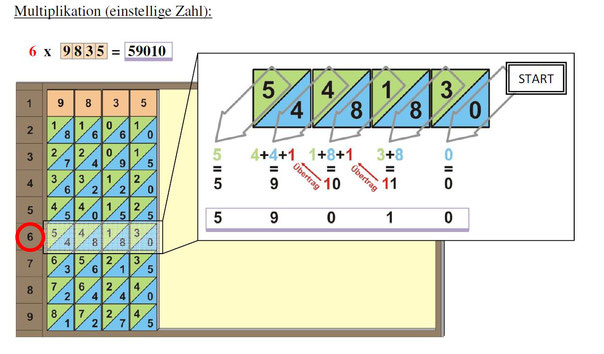
Die Idee zu den Stäbchen habe ich aus der Methode der zweidimensionalen Gittermultiplikation abgeleitet, die sie sicher kennen. Man zeichnet ein Rechteck, schreibt die Produktfaktoren oben und rechts an den Rändern an und die Teilprodukte der Ziffern in das Gitter. Dann wird nur noch diagonal addiert. Man muss das Gitter nur in Streifen schneiden und sich auf einen einstelligen Faktor beschränken.
Ich selbst hielt nichts Besonderes von meiner Erfindung, als ich sie jedoch Freunden zeigte, haben die mich gedrängt, meine Informationen zu diesen Stäbchen unbedingt zu veröffentlichen.
Also habe ich ein kleines Buch über die Rabdologia geschrieben, das kam 1617 heraus mit einem erklärenden Titel: Rabdologiae seu numerationis per virgulas libri duo.
(er zeigt das Buch)
Das ganze System besteht aus ein paar Stäben mit dem kleinen Einmaleins.
(Er zeigt einen Stabsatz)
Auf einer Stabseite stehen untereinander die 2- bis 9-fachen der Zahl oben. Wenn man die Stäbe zusammen legt, sodass die Ziffern oben eine mehrstellige Zahl ergeben, dann kann man in den Zeilen weiter unten die 2- bis 9-fachen dieser Zahl ablesen. Man muss nämlich nur die diagonalen Ziffern mit ihrem Übertrag addieren.
Wichtig ist, dass man das kleine Einmaleins nicht unbedingt kennen muss, man muss nur addieren können.
Dividieren ist auch nicht schwer, weil man sich die Vielfachen des gegebenen Quotienten zusammenstellen kann.
Zwei weitere Stäbe sind hilfreich bei der Berechnung von Quadrat- und Kubikwurzeln.
Die Stäbe werden zweckmäßig aus Holz oder aus Knochen bzw. Elfenbein hergestellt. Manche nennen sie deswegen Napier's bones. Ich weiß nicht so recht, was ich davon halten soll, da hat sich jemand einen Scherz gemacht.
Wenn man das Prinzip der Rechenstäbchen auf zwei mehrstellige Produktfaktoren erweitern will kommt man zu einem System, das ich Promptuarium Multiplicationis genannt habe.
Promptuarium ist --- kein von mir erfundener Name, den gibts schon, er bedeutet soviel wie Lager, sofort verfügbar.
Es handelt sich um waagerechte und senkrechte Stäbe. Wenn man diese Stäbe übereinander legt, erhält man das Bild einer vollständigen Gittermultiplikation.
In der Arithmetica localis zeige ich, dass man unabhängig von einem Stellenwertsystem Zahlen auch in einem Additionssystem grafisch darstellen kann und mit Bewegungen in einem zweidimensionalen System rechnen kann.
Inwieweit meine Rechenhilfen von Rechnern angenommen werden, kann ich nicht beurteilen. Ich habe sie nur zur Verfügung gestellt.

Der weitere Weg und die Wertung der Rechenhilfen sei hier kurz dargestellt:
Napiers Rechenstäbchen verbreiten sich rasch, ein Jahr später 1618 bereits erscheint die deutsche Version der „Künstlichen Rechenstäblein“ mit Beschreibung von Franz Kessler (1580 – 1650). Weitere Ausgaben in anderen Sprachen folgen.
Schon 1624 hat Wilhelm Schickard eine Rechenmaschine mit Zehnerübertrag auf Basis der Napier´schen Rechenstäbchen skizziert.
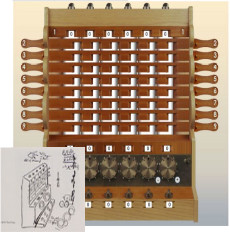
Napiers Rechenstäbchen erlangen einen hohen Bekanntheitsgrad, sie fehlen in der Folgezeit in keinem Lehrbuch der Arithmetik.
Ab Ende des 19. / Anfang des 20. Jahrhunderts wird diese Idee in zahlreichen Patenten für Rechenhilfen wieder aufgenommen. Deren Anschaffungskosten waren nämlich viel geringer als die hohen Anschaffungskosten von Rechenmaschinen.
Das Promptuarium hingegen bleibt so gut wie unbekannt. Es ist viel zu groß und unhandlich.
Die Arithmetica localis ist eine rechentechnische Spielerei, sie wird in der nachfolgenden Literatur nicht mehr aufgegriffen.
Neben den Rechenhilfen soll Napiers weitere Wirkung auf die Mathematik nicht unerwähnt bleiben.
Sir John, Sie haben der Mathematik noch andere Impulse gegeben.
(überlegt)
Was habe ich sonst noch auf dem Gebiet der Mathematik gemacht...
Anfänglich hatte ich an einer ars logistica gearbeitet, die die Methodik der Arithmetik und der Algebra umfasst. Ich hielt dann aber die Arbeit an den Logarithmen für wichtiger und habe das Werk zurückgestellt. Ich weiß noch nicht, wann ich es herausbringen werde.
Zum Dezimalbruch:
die Darstellung des Dezimalbruchs war bisher uneinheitlich und hat deshalb Schwierigkeiten bereitet.
In Hexadezimalzahlen wird eine Stellenkennzeichnung verwendet, etwa 7°22''.
Simon Stevin hat dieses Verfahren auf Dezimalbrüche umgesetzt mit Stellenkennzeichnungen, aber die sind umständlich
Ich bevorzuge wie schon andere auch einen Dezimalpunkt. Die Stellen ergeben sich dann aus der Anordnung der Ziffern und müssen nicht gekennzeichnet werden.
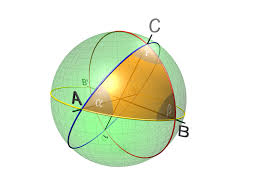
In der Trigonometrie habe ich mich mit sphärischen Dreiecken befasst. Sie sind wichtig für Navigatoren und Astronomen. Mein Ziel war, die Beziehungen so umzustellen, dass sie dem Gebrauch der Logarithmen angepasst sind. Zudem konnte ich neue Beziehungen in sphärischen Dreiecken formulieren.

Die Ars logistica wurde erst Jahrhunderte später veröffentlicht, sodass sie trotz ihrer Modernität keinen Einfluss auf die zeitgenössische Mathematik leisten konnte.
Ich komme nun zur Bewertung von Napiers Werk für die folgenden Jahrhunderte.
John Napier hat mit den Logarithmen und den von ihm entworfenen Rechenstäbchen die Rechentechnik der nachfolgenden Jahrhunderte maßgeblich beeinflusst. Das betrifft vornehmlich aber nicht ausschließlich Berechnungen in der Astronomie, in der Kartographie und in der Navigation.
Logarithmen sind die Voraussetzung für die Entwicklung der danach 350 Jahre lang genutzten Rechenschieber und Logarithmentafeln (von denen über 3000 in der Collectanea de Logarithmis dokumentiert sind)
Logarithmen sind Bestandteil vieler Naturgesetze. Logarithmen sind auf vielfache Weise berechnet worden und haben dadurch die mathematische Denke bereichert.
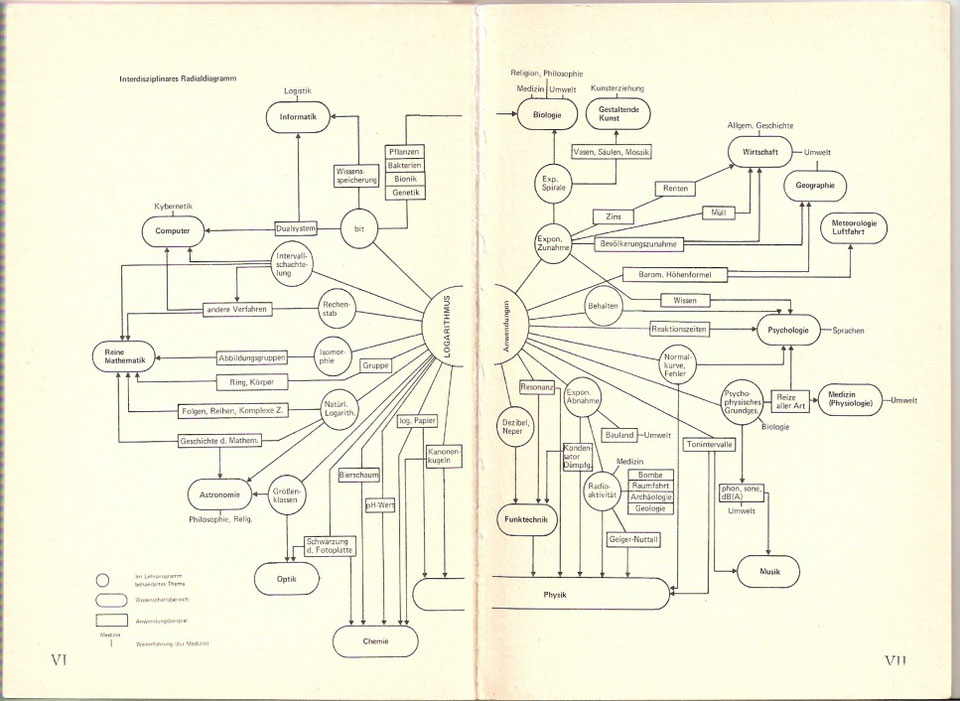
Logarithmen sind heutzutage immer noch im Einsatz, z.B.
• beim Bestimmen des pH-Wertes in der Chemie
• bei der Berechnung der Erdbebenstärke auf der Richter Skala
• bei der Berechnung des radioaktiven Zerfalls
• bei der Lautstärkebestimmung mit Dezibel
• um den Zusammenhang zwischen Reiz und Empfindung (Weber-Fechner-Gesetz) darzustellen
• für Zins- und Zinseszins-Berechnungen
Logarithmen spielen außerdem in der Musik/Akustik und im High Performance Computing eine wichtige Rolle.
Bei Betrachtung dieses umfangreichen und wichtigen mathematischen Werkes eines einzelnen Mannes stellt sich eine Frage, die er selbst beantworten soll.
Mein größtes Werk?
Da gibt es keine Frage, das war die Offenbarung des Johannes.
(Vorhang)

Vielen Dank für Ihr Kommen und Ihre Aufmerksamkeit
Bildquellen:
1.
Hamann, Christel: http://www.rechnerlexikon.de/artikel/Differenzenmaschine_Hamann
2. Thompson, A.J.: http://www.rechnerlexikon.de/artikel/Differenzenmaschine_Thompson
3. Röttel, Karl: Lehrprogramm „Logarithmus – Einführung“, 2. Auflage München 1979
4. John Napier portrait with Courtesy The University of Edinburgh
5. Wikipedia
Für den Dialog © Klaus Kühn und Stephan Weiss